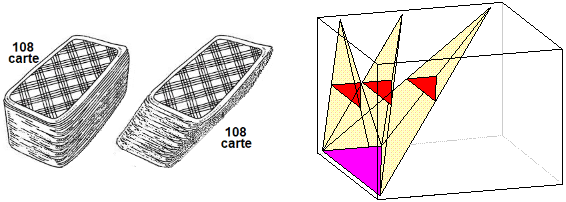

Il volume di un solido non cambia se lo sezioniamo con un fascio di piani tra loro paralleli e, a partire dal primo piano che lo taglia, ne spostiamo via via le sezioni con un movimento continuo, come nel caso del mazzo di carte raffigurato sopra a sinistra.
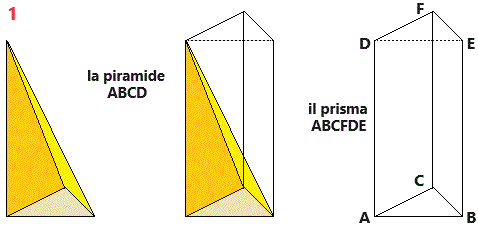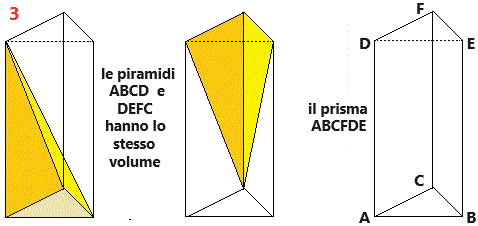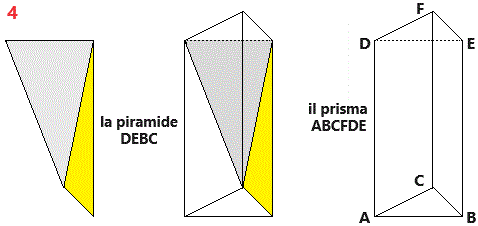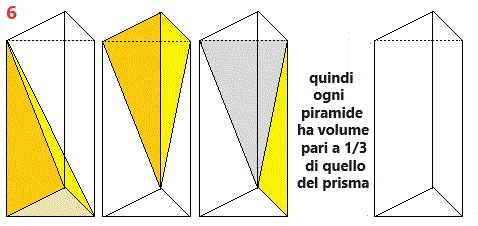
Analogamente, come raffigurato a destra, piramidi di uguale base ed uguale altezza hanno il medesimo volume. Ma qual è il volume di una piramide? Iniziamo con le piramidi a base triangolare.
|
Un qualunque poligono può essere scomposto in triangoli, quindi ogni prisma può essere scomposto in prismi triangolari. La proprietà (volume = prodotto dell'area di base per l'altezza) si estende quindi facilmente ad ogni piramide. La stessa cosa, ovviamente, vale per i coni (caso limite delle primadi al crescere del numero di lati). Dunque, riassumendo, come l'area di un triangolo con un lato lungo L e l'altezza relativa lunga h è L·h/2, così il volume di una piramide o di un cono di area di base A ed altezza h è pari a A·h/3. | 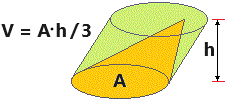 |
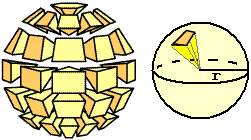 |
Il volume di una sfera? Approssimo la sfera con l'unione di tante piramidi. Al crescere del numero di queste piramidi, e al decrescere della loro area di base, il volume di questa unione tende al volume della sfera. La loro altezza tende a coincidere con il raggio R della sfera, mentre la somma delle superfici di base tende a coincidere con la superficie totale della sfera (4·πR²). Quindi il volume della sfera è 4/3·πR³. |